Introduction to accessibility: calculating accessibility measures • accessibility

accessibility is an R package that offers a set of fast and convenient functions to calculate multiple transport accessibility measures. Given a pre-computed travel cost matrix and a land use dataset, the package allows one to calculate active and passive accessibility levels using multiple accessibility metrics, such as cumulative opportunities (using either a travel cost cutoff or a travel cost interval), minimum travel cost to closest N number of activities, gravitational measures and different floating catchment area methods. This vignette briefly overviews the package with a few reproducible examples.

Installation

Before using accessibility please make sure that you have it installed in your computer. You can download either the most stable version from CRAN…

install.packages("accessibility")

…or the development version from GitHub.

# install.packages("remotes")
remotes::install_github("ipeaGIT/accessibility")

Overview of the package

As of the time of writing this vignette, the accessibility package includes five different functions to calculate accessibility:

cost_to_closest() - calculates the minimum travel cost to the closest n number of opportunities.
cumulative_cutoff() - calculates the frequently used threshold-based cumulative opportunities measure.
cumulative_interval() - calculates accessibility as the median/mean (or any other summary measure, really) number of opportunities that can be reached within a cost interval.
gravity() - calculates gravity-based accessibility, taking a decay function specified by the user (more on that in a few paragraphs).
floating_catchment_area() - calculates accessibility taking into account the effects of competition for opportunities with different floating catchment area measures.

You may have noticed that we’ve mentioned a few times that the functions calculate accessibility using travel cost, and not travel time. That’s because we’re treating costs here in its generic sense: anything that increases the impedance from an origin to a destination, such as travel time, monetary costs, distances, risk perception, etc., can be considered a generic cost.

The gravity() and floating_catchment_area() functions can use different decay functions when estimating accessibility levels. These decay functions effectively weigh the number of opportunities in a destination by a factor that depends on the travel cost between the origin and the destination. For convenience, the package currently includes the following decay functions:

decay_binary() - binary decay function (the one used in cumulative opportunities measures).
decay_exponential() - negative exponential decay function.
decay_linear() - linear decay function (weights decay linearly from 1 to 0 until a specific travel cost cutoff is reached).
decay_power() - inverse power decay function.
decay_stepped() - stepped decay function (similar to decay_binary(), but can take an arbitrary number of steps, instead of a single one).

The users can also specify their own custom decay functions, if they need to use functions currently not included in the package. For more details on this, please read the decay functions vignette.

Demonstration on sample data

Enough talking. Let’s demonstrate some of the key features of the package. First we’ll need to load the libraries we’ll be using:

library(accessibility)
library(data.table)
library(ggplot2)
library(sf)

Data requirements

To use accessibility, you will need a pre-computed travel cost matrix and some land use data (e.g. location of jobs, healthcare, population, etc.). As mentioned before, travel costs can be presented in terms of travel times, distances or monetary costs, for example. This dataset must be structured in a data.frame containing, at least, the columns from_id, to_id and the travel cost between each origin-destination pair.

Your data should look similar to this sample dataset with public transport travel times for the city of Belo Horizonte, Brazil, included in the package for demonstration purposes¹.

data_dir <- system.file("extdata", package = "accessibility")

travel_matrix <- readRDS(file.path(data_dir, "travel_matrix.rds"))
head(travel_matrix)
#>            from_id           to_id travel_time
#>             <char>          <char>       <num>
#> 1: 89a88cdb57bffff 89a88cdb57bffff         5.8
#> 2: 89a88cdb57bffff 89a88cdb597ffff        47.0
#> 3: 89a88cdb57bffff 89a88cdb5b3ffff        48.0
#> 4: 89a88cdb57bffff 89a88cdb5cfffff        47.0
#> 5: 89a88cdb57bffff 89a88cd909bffff        64.0
#> 6: 89a88cdb57bffff 89a88cd90b7ffff        59.0

The land use data must also be structured in a data.frame and must contain an id column, referring to the ids listed in the travel matrix, and the number of opportunities/facilities/services in each spatial unit. The sample dataset we’ll be using looks like this:

land_use_data <- readRDS(file.path(data_dir, "land_use_data.rds"))
head(land_use_data)
#>                 id population  jobs schools income_per_capita income_decile
#>             <char>      <int> <int>   <int>             <num>        <fctr>
#> 1: 89a881a5a2bffff        381   180       0           22369.1            10
#> 2: 89a881a5a2fffff        269   134       0            3205.1             9
#> 3: 89a881a5a67ffff        929   143       0           11394.0            10
#> 4: 89a881a5a6bffff        249    61       0            3659.8             9
#> 5: 89a881a5a6fffff        176    11       0            4905.1            10
#> 6: 89a881a5b03ffff        681  1071       0            2200.2             8

Minimum travel cost

cost_to_closest() calculates the minimum travel cost to a given number of opportunities. Much like the other functions we’ll be demonstrating in this section, it takes as inputs the travel matrix and land use datasets, the name of the column in the latter with the opportunities to be considered and the name of the column in the former with the travel cost to be considered. Additionally, it takes the minimum number of opportunities to be considered. Here’s how calculating the time from each origin in Belo Horizonte to the closest school looks like:

mtc <- cost_to_closest(
  travel_matrix,
  land_use_data,
  opportunity = "schools",
  travel_cost = "travel_time",
  n = 1
)
head(mtc)
#> Key: <id>
#>                 id travel_time
#>             <char>       <num>
#> 1: 89a881a5a2bffff          29
#> 2: 89a881a5a2fffff          24
#> 3: 89a881a5a67ffff          28
#> 4: 89a881a5a6bffff          33
#> 5: 89a881a5a6fffff          32
#> 6: 89a881a5b03ffff          17

Cutoff-based cumulative opportunities

cumulative_cutoff() calculates the traditional cumulative opportunities measure, indicating the number of opportunities that are accessible within a given travel cost threshold. In this example, we estimate how many jobs can be reached from each origin with trips taking up to 30 minutes of travel time.

cum_cutoff <- cumulative_cutoff(
  travel_matrix,
  land_use_data,
  opportunity = "jobs",
  travel_cost = "travel_time",
  cutoff = 30
)
head(cum_cutoff)
#>                 id  jobs
#>             <char> <int>
#> 1: 89a881a5a2bffff 14561
#> 2: 89a881a5a2fffff 29452
#> 3: 89a881a5a67ffff 16647
#> 4: 89a881a5a6bffff 10700
#> 5: 89a881a5a6fffff  6669
#> 6: 89a881a5b03ffff 37029

Let’s say that we wanted to, instead, calculate passive accessibility - i.e. by how many people each destination can be reached within a given travel cost. Doing so requires very few changes to the call: just change the “opportunity” column to "population" and set active (TRUE by default) to FALSE.

passive_cum_cutoff <- cumulative_cutoff(
  travel_matrix,
  land_use_data,
  opportunity = "population",
  travel_cost = "travel_time",
  cutoff = 30,
  active = FALSE
)
head(passive_cum_cutoff)
#>                 id population
#>             <char>      <int>
#> 1: 89a881a5a2bffff      11053
#> 2: 89a881a5a2fffff      31903
#> 3: 89a881a5a67ffff      12488
#> 4: 89a881a5a6bffff      14474
#> 5: 89a881a5a6fffff      15053
#> 6: 89a881a5b03ffff      69582

The active parameter is available in most other accessibility functions as well (with the exception of floating_catchment_area()), making it very easy to calculate both active and passive accessibility.

Interval-based cumulative opportunities

cumulative_time_interval() calculates the interval-based cumulative opportunities measure. This measure, developed by Tomasiello et al. (2023), mitigates the impacts of arbitrary choices of cost cutoffs, one of the main disadvantages of the traditional threshold-based cumulative opportunities measure. Given a cost interval, it calculates several accessibility estimates within the interval and summarizes it using a user-specified function. In the example below, we calculate the average number of accessible jobs considering multiple minute-by-minute time thresholds between 40 and 60 minutes.

cum_interval <- cumulative_interval(
  travel_matrix = travel_matrix,
  land_use_data = land_use_data,
  opportunity = "jobs",
  travel_cost = "travel_time",
  interval = c(40, 60),
  summary_function = base::mean
)
head(cum_interval)
#>                 id   jobs
#>             <char>  <int>
#> 1: 89a88cdb57bffff 311965
#> 2: 89a88cdb597ffff 249416
#> 3: 89a88cdb5b3ffff 302515
#> 4: 89a88cdb5cfffff 373386
#> 5: 89a88cd909bffff 308429
#> 6: 89a88cd90b7ffff 344118

Gravity measures

gravity() calculates gravity-based measures - i.e. measures in which the weight of opportunities is gradually discounted as the travel cost increases. Of course, several different decay functions can be used to so, each one of them with a range of possible different parameters. In order to accommodate such generalization, the function takes the decay function to be used as a parameter.

In the example below, we calculate accessibility using a negative exponential function with a decay_value (usually referred as the in its formulation) of 0.2. Please see the vignette on decay functions for more information on the decay functions shipped with the package and how to use custom functions.

negative_exp <- gravity(
  travel_matrix,
  land_use_data,
  opportunity = "schools",
  travel_cost = "travel_time",
  decay_function = decay_exponential(decay_value = 0.2)
)
head(negative_exp)
#>                 id    schools
#>             <char>      <num>
#> 1: 89a88cdb57bffff 0.03041853
#> 2: 89a88cdb597ffff 1.15549493
#> 3: 89a88cdb5b3ffff 0.56519126
#> 4: 89a88cdb5cfffff 0.19852152
#> 5: 89a88cd909bffff 0.41378042
#> 6: 89a88cd90b7ffff 0.95737555

Floating catchment area

floating_catchment_area() calculates accessibility accounting for competition of resources using different floating catchment area (FCA) methods. The FCA family includes several different methods, which can be specified using the method parameter. As of the time of writing this vignette, the package supports two different methods:

2-Step Floating Catchment Area ("2sfca") - the first metric in the FCA family, originally proposed by Luo and Wang (2003).
Balanced Floating Catchment Area ("bfca") - takes competition affects into account while correcting for issues of inflation of demand and service levels. Originally proposed by Paez, Higgins, and Vivona (2019) and named in Pereira et al. (2021).

Please note that, since FCA measures consider competition effects, we have to specify which column in the land use dataset represents the population competing for opportunities with the demand parameter. The function also supports different decay functions. In the example below, we calculate accessibility to jobs using the BFCA method, considering that the entire population of the city compete for these jobs and using a negative exponential decay function.

bfca <- floating_catchment_area(
  travel_matrix,
  land_use_data,
  opportunity = "jobs",
  travel_cost = "travel_time",
  demand = "population",
  method = "bfca",
  decay_function = decay_exponential(decay_value = 0.5)
)
head(bfca)
#>                 id       jobs
#>             <char>      <num>
#> 1: 89a88cdb57bffff 0.10280082
#> 2: 89a88cdb597ffff 0.30930287
#> 3: 89a88cdb5b3ffff 0.07288551
#> 4: 89a88cdb5cfffff 0.09759117
#> 5: 89a88cd909bffff 0.07390234
#> 6: 89a88cd90b7ffff 1.22525579

Spatial availability

spatial_availability() also calculates accessibility considering competition effects, though using the spatial availability measure proposed by Soukhov et al. (2023). The results from this metric are proportional both to the demand in each origin and the travel cost it takes to reach the destinations. As with the FCA function, we have to specify the column in the land use dataset that contains the population competing for opportunities and we can use different decay functions to calculate the impedance between origin-destination pairs.

spatial_avlblt <- spatial_availability(
  travel_matrix,
  land_use_data,
  opportunity = "jobs",
  travel_cost = "travel_time",
  demand = "population",
  decay_function = decay_exponential(decay_value = 0.1)
)
head(spatial_avlblt)
#>                 id     jobs
#>             <char>    <num>
#> 1: 89a88cdb57bffff 186.0876
#> 2: 89a88cdb597ffff 140.0738
#> 3: 89a88cdb5b3ffff 736.5830
#> 4: 89a88cdb5cfffff 900.9284
#> 5: 89a88cd909bffff   0.0000
#> 6: 89a88cd90b7ffff 204.7962

Balancing cost

balancing_cost() calculates the balancing cost accessibility measure. Originally proposed by Barboza et al. (2021) under the name “balancing time”, this metric is defined as the travel cost required to reach as many opportunities as the number of people in a given origin. Just like the previous two functions, balancing_cost() also includes a parameter to specify the population competing for opportunities.

The function also includes a cost_increment parameter, that should be used to specify the increment that defines the travel cost distribution from which the potential balancing costs will be picked. For example, an increment of 1 (the default) tends to suit travel time distributions, meaning that the function will first check if any origins reach their balancing cost with a travel time of 0 minutes, then 1 minute, 2 minutes, 3, 4, …, etc. On the other hand, an increment of 1 might be too big for a distribution of monetary costs, which could possibly benefit from a smaller increment of 0.05 (5 cents), for example. Such increment results in the function looking for balancing costs first at a monetary cost of 0, then 0.05, 0.10, …, etc. In the example below, we use the default cost increment of 1.

bal_cost <- balancing_cost(
  travel_matrix,
  land_use_data,
  opportunity = "jobs",
  travel_cost = "travel_time",
  demand = "population"
)
head(bal_cost)
#> Key: <id>
#>                 id travel_time
#>             <char>       <num>
#> 1: 89a881a5a2bffff          15
#> 2: 89a881a5a2fffff          13
#> 3: 89a881a5a67ffff          23
#> 4: 89a881a5a6bffff           7
#> 5: 89a881a5a6fffff          10
#> 6: 89a881a5b03ffff           6

Visualize results

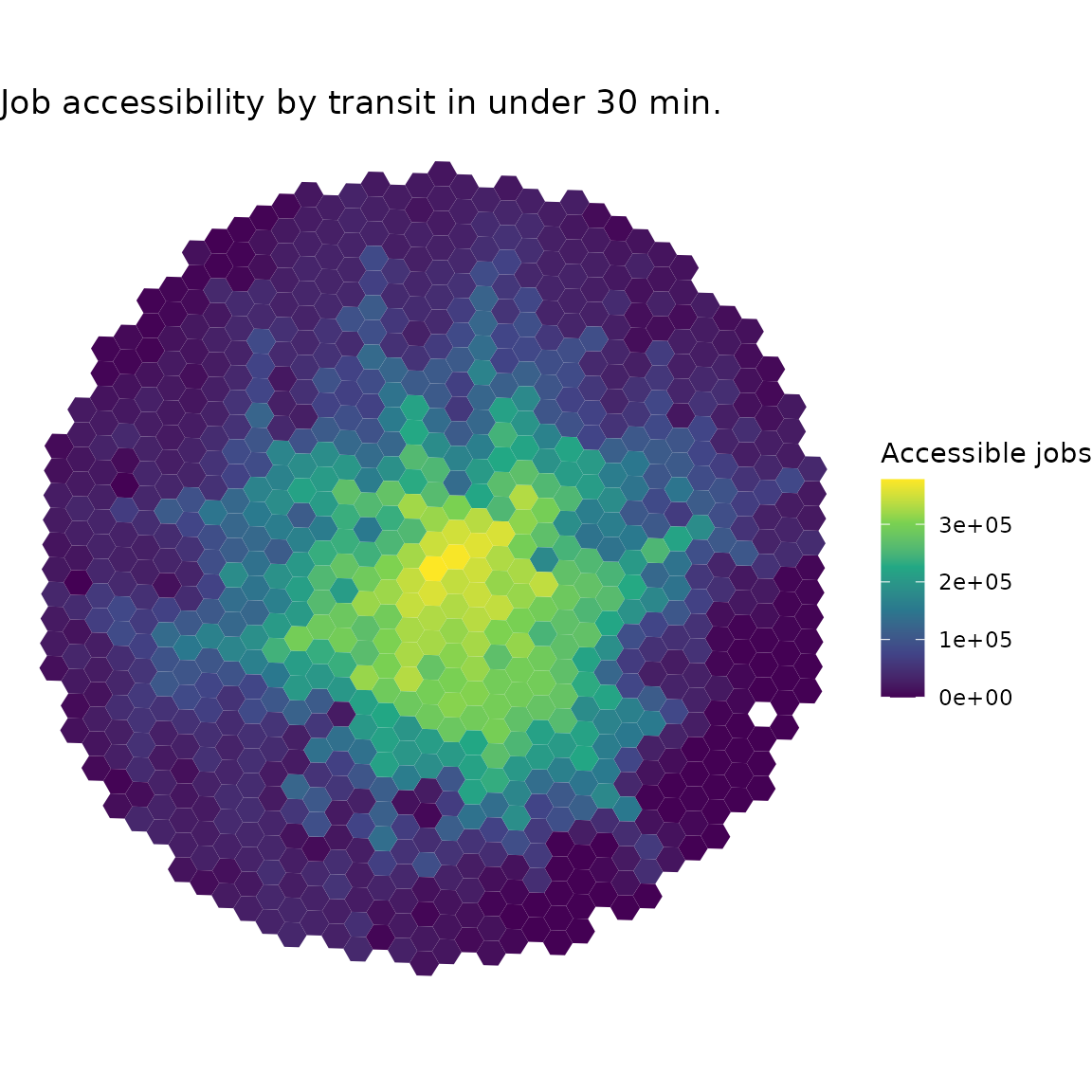
If you have the spatial data of your origins/destinations, you can easily merge it with the accessibility to create spatial visualizations of the results. The example below quickly shows how to create a simple map using ggplot2.

grid <- system.file("extdata/grid_bho.rds", package = "accessibility")
grid <- readRDS(grid)

spatial_data <- merge(grid, cum_cutoff, by = "id")

ggplot() +
  geom_sf(data = spatial_data, aes(fill = jobs), color = NA) +
  labs(
    title = "Job accessibility by transit in under 30 min.",
    fill = "Accessible jobs"
  ) +
  scale_fill_viridis_c() +
  theme_void()

References

Barboza, Matheus H. C., Mariana S. Carneiro, Claudio Falavigna, Gregório Luz, and Romulo Orrico. 2021. “Balancing Time: Using a New Accessibility Measure in Rio de Janeiro.” Journal of Transport Geography 90 (January): 102924. https://doi.org/10.1016/j.jtrangeo.2020.102924.

Luo, Wei, and Fahui Wang. 2003. “Measures of Spatial Accessibility to Health Care in a GIS Environment: Synthesis and a Case Study in the Chicago Region.” Environment and Planning B: Planning and Design 30 (6): 865–84. https://doi.org/10.1068/b29120.

Paez, Antonio, Christopher D. Higgins, and Salvatore F. Vivona. 2019. “Demand and Level of Service Inflation in Floating Catchment Area (FCA) Methods.” Edited by Tayyab Ikram Shah. PLOS ONE 14 (6): e0218773. https://doi.org/10.1371/journal.pone.0218773.

Pereira, Rafael H. M., Carlos Kauê Vieira Braga, Luciana Mendes Servo, Bernardo Serra, Pedro Amaral, Nelson Gouveia, and Antonio Paez. 2021. “Geographic Access to COVID-19 Healthcare in Brazil Using a Balanced Float Catchment Area Approach.” Social Science & Medicine 273 (March): 113773. https://doi.org/10.1016/j.socscimed.2021.113773.

Soukhov, Anastasia, Antonio Páez, Christopher D. Higgins, and Moataz Mohamed. 2023. “Introducing Spatial Availability, a Singly-Constrained Measure of Competitive Accessibility.” Edited by Jun Yang. PLOS ONE 18 (1): e0278468. https://doi.org/10.1371/journal.pone.0278468.

Tomasiello, Diego Bogado, Daniel Herszenhut, João Lucas Albuquerque Oliveira, Carlos Kaue Vieira Braga, and Rafael H. M. Pereira. 2023. “A Time Interval Metric for Cumulative Opportunity Accessibility.” Applied Geography 157 (August): 103007. https://doi.org/10.1016/j.apgeog.2023.103007.

If you would like to calculate such travel cost matrices yourself, there are several computational packages to do that in R, such as r5r, dodgr, gtfsrouter, hereR and opentripplanner.↩︎